Finding factorial is important in several domains. For instance, it can be used for solving complex combinatorial problems to optimize algorithms. So, in today’s guide, we will learn different approaches that can assist you in finding the factorial of a number in your Python program.
From iteration, and recursion, to the built-in functions, and dynamic programming, we will cover each technique with practical examples. So, let’s start the guide!
Why Find the Factorial of a Number in Python
In different scenarios related to programming, calculating the factorial of a number is considered a fundamental operation. It offers practical solutions in different domains and also holds a significant place in mathematical operations.
Here are some of the relevant use cases:
- Combinatorial Problems – Factorials play a vital role in solving combinatorial problems, such as counting permutations and combinations.
- Probability Calculations – Probability calculations often involve factorials when calculating the number of possible outcomes.
- Algorithm Design – Some algorithms, like those involving recursive processes, require factorial calculations to solve specific subproblems.
- Statistical Analysis – Factorials are used in statistical analysis, particularly in permutations and arrangements of data sets.
- Data Validation – Factorial calculations can assist in validating data sets and ensuring the accuracy of results.
- Iterative Processes – In iterative processes that involve counting or arranging elements, factorials provide essential insights.
How to Find Factorial of a Number in Python
For the purpose of finding the factorial of a number in Python, you can use:
- Iteration
- Recursion
- “
math.factorial()” function - Dynamic Programming
Let’s explain each of the listed approaches practically!
1. Using Iteration
Iteration is one of the simplest approaches for finding the factorial of a number. In this method, a for loop is used for looping and multiplying the consecutive integers from 1 to the specified numbers.
Additionally, this method is easy to implement, which makes it suitable for beginners and small inputs.
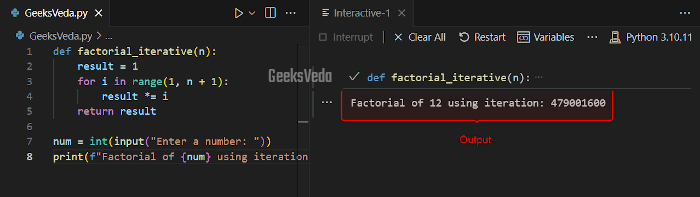
For instance, in the following program, we will define a function named “factorial_iterative()” that will calculate the factorial of a number. It asks the users to enter a number with the input() function and then calculates its factorial by multiplying integers from 1 to the given number.
def factorial_iterative(n):
result = 1
for i in range(1, n + 1):
result *= i
return result
num = int(input("Enter a number: "))
print(f"Factorial of {num} using iteration: {factorial_iterative(num)}")
For instance, we have entered 12 to calculate its factorial. Resultantly, “479001600” will be displayed on the console as 12’s factorial.
2. Using Recursion Approach
The recursion approach is based on defining a function that invokes itself with the updated parameters until it reaches the base case, which is factorial of 1. This method reflects the mathematical nature of the factorials.
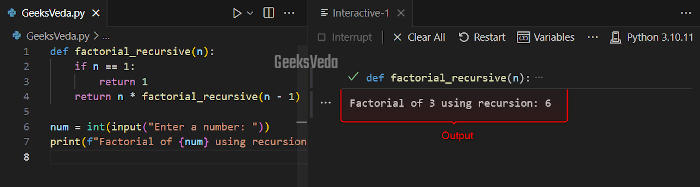
Here, we will define a function named “factorial_recursive()” that defines the base case (n == 1) and the recursive case “(n * factorial_recursive(n – 1))” which eventually reaches the base case and computes the factorial.
def factorial_recursive(n):
if n == 1:
return 1
return n * factorial_recursive(n - 1)
num = int(input("Enter a number: "))
print(f"Factorial of {num} using recursion: {factorial_recursive(num)}")
3. Using the “math.factorial()” Function
Python’s “math” module provides a “factorial()” function that conveniently computes the factorial of a given number. It enables you to get rid of the hassle of writing down your own factorial logic.
More specifically, this “math.factorial()” function is highly accurate and efficient and recommended for those use cases where simplicity and precision are needed.
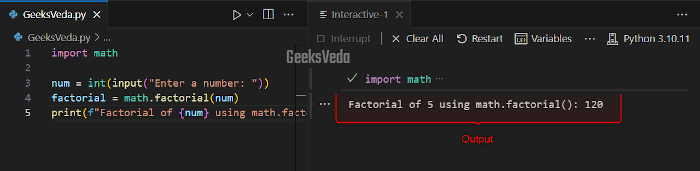
Now, we will first import the “math” module and then invoke the “math.factorial()” method for calculating the factorial of the number specified by the user.
import math
num = int(input("Enter a number: "))
factorial = math.factorial(num)
print(f"Factorial of {num} using math.factorial(): {factorial}")
4. Using Dynamic Programming
Dynamic programming can be also applied to finding the factorial of a number. This technique is primarily utilized in scenarios where repetitive calculations occur. It also minimizes the redundant calculations and accelerates the factorial computation which makes it a robust method for larger inputs.
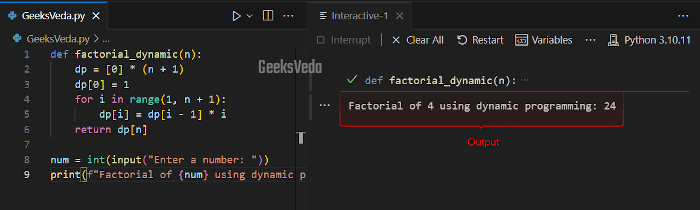
In the following code, the “factorial_dynamic()” function uses an array named “do” to store the intermediate results. This makes sure that each factorial calculation is built upon the previous ones.
def factorial_dynamic(n):
dp = [0] * (n + 1)
dp[0] = 1
for i in range(1, n + 1):
dp[i] = dp[i - 1] * i
return dp[n]
num = int(input("Enter a number: "))
print(f"Factorial of {num} using dynamic programming: {factorial_dynamic(num)}")
Choosing the Right Method for Finding the Factorial of a Number
Let’s check out the provided comparison for selecting the best method to find the factorial of a number:
| Method | Advantages | Disadvantages | Use Cases |
| Using Iteration |
|
|
Quick calculations of factorials for smaller numbers or educational purposes. |
| Using Recursion |
|
|
Learning recursion, solving problems with smaller inputs, and mathematical exploration. |
| Using math.factorial() |
|
May not provide a deeper understanding of factorial calculation. | Simplicity and accuracy in scenarios requiring precise factorial calculations. |
| Using Dynamic Programming |
|
Requires understanding of dynamic programming concepts. | Handling larger inputs efficiently, especially in scenarios with repetitive calculations. |
That’s all from today’s guide related to finding the factorial of a number in Python.
Conclusion
Python offers different versatile methods that allow you to handle different types of manipulation related to numbers. More specifically, it enables you to find the factorial of a number using several approaches.
From the simplicity of the iteration to the efficiency of the built-in functions and dynamic programming, each method offers its unique advantages based on the use cases.
Choose the one wisely to optimize your code and solve complex mathematical problems that are based on calculating factorial.
Want to explore and learn more related to Python, do check out our dedicated Python Tutorial Series!
